Joachim Kuczynski, 01 November 2025
Net Income
With the abbreviations 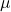 … net income, S … sales, F … fix expenses, V … variable expenses, A … depreciation and amortization, T … taxes, I … interests for debt and X … tax shield we can define net income by:
… net income, S … sales, F … fix expenses, V … variable expenses, A … depreciation and amortization, T … taxes, I … interests for debt and X … tax shield we can define net income by:
(1) 
Let 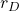 be the interest rate for debt and
be the interest rate for debt and 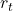 be the incremental tax rate. We assume that we get full tax shield of
be the incremental tax rate. We assume that we get full tax shield of 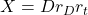 . Taxes
. Taxes 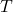 are paid on EBIT, that means
are paid on EBIT, that means 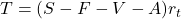 .
. 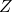 =equity+debt is the asset or enterprise value and d is the debt ratio,
=equity+debt is the asset or enterprise value and d is the debt ratio, 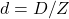 . Substituting that in the previous expression we obtain:
. Substituting that in the previous expression we obtain:
(2) 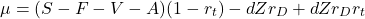
Summarizing the terms leads to:
(3) 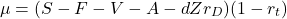
Beta of a weighted sum is the weighted sum of the components’ betas, shown in the post “Portfolio Beta”. Thus we get an equation for the betas:
(4) 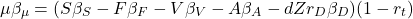
We assume that fix expenses (F), depreciation, amortization (A) and debt (D) have no correlation to the market return rate, 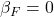 ,
, 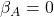 ,
, 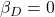 . Variable expenses should have the same correlation to market development as sales, that gives
. Variable expenses should have the same correlation to market development as sales, that gives 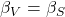 . We obtain:
. We obtain:
(5) 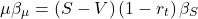
Substituting 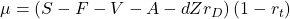 leads to:
leads to:
(6) 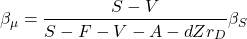
Rearranging the terms shows:
(7) 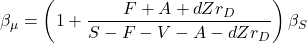
Return on Equity
Return on equity measures relative equity increase. It is defined by:
(8) 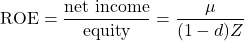
With the substitution of 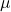 we obtain:
we obtain:
(9) 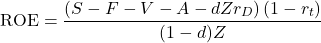
We want to link the beta of ROE to the beta of net income. We take the definition of 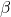 with its bilinearity of covariance and get:
with its bilinearity of covariance and get:
(10) 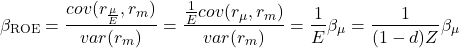
Hence we get 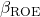 as function of
as function of 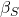 :
:
(11) 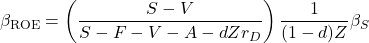
(12) 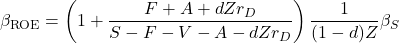
This is the relationship of the ROE beta and the sales beta. It depends on several variables, but especially on fixed expenses 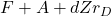 .
.
Releveraging Equity Return Rate and WACC
An equity investor wants to know which return rate market provides at the same risk (volatility) level as our investigated investment. The WACC after taxes of the appropriate market portfolio is given by:
(13) 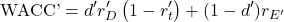
I indicate all market portfolio parameters with a line on the top. 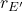 ist the required return rate of an incremental equity investor. This is the return rate of the completely diversified market portfolio of the appropriate industry segment. The Capital Asset Pricing Model (CAPM) states that
ist the required return rate of an incremental equity investor. This is the return rate of the completely diversified market portfolio of the appropriate industry segment. The Capital Asset Pricing Model (CAPM) states that 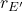 can be approximated by a linear function of
can be approximated by a linear function of  by a given market return rate
by a given market return rate 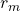 :
:
(14) 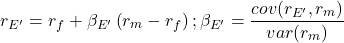
 is the average equity
is the average equity 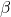 of an market portfolio representing the investigated investment. It is based on an averaged financial and operating leverage of the market portfolio. If these parameters do not match capital and cost structure of the considered investment, you have to “releverage”
of an market portfolio representing the investigated investment. It is based on an averaged financial and operating leverage of the market portfolio. If these parameters do not match capital and cost structure of the considered investment, you have to “releverage”  .
.
Operating leverage: We have a look at the relationship of  and
and 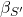 :
:
(15) 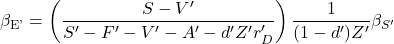
 is provided by an official data collection in most cases. With the other data from the market portfolio we can calculate
is provided by an official data collection in most cases. With the other data from the market portfolio we can calculate 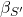 :
:
(16) 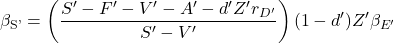
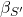 is the linear approximated change of sales because of a change in market return rate
is the linear approximated change of sales because of a change in market return rate 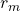 .
. 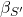 does not depend on
does not depend on 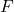 ,
, 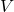 ,
, 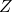 ,
, 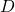 ,
, 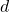 and
and 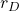 .
. 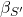 is the same for all combinations of these parameters, that means
is the same for all combinations of these parameters, that means  . Now we take the parameters of the investment, to which we want to adjusted
. Now we take the parameters of the investment, to which we want to adjusted 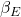 . With the
. With the 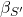 from the previous equation we obtain the adjusted
from the previous equation we obtain the adjusted 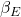 :
:
(17) 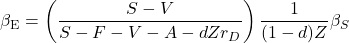
With this 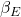 we can calculate the new equity return rate
we can calculate the new equity return rate 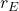 :
:
(18) 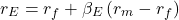
After the releveraging process we get the releveraged WACC with the appropriate 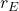 :
:
(19) 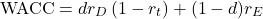
![]() and equity return rates
and equity return rates ![]() .
. ![]() indicates the
indicates the ![]() -th of
-th of ![]() data pairs.
data pairs. ![]() and
and ![]() are the arithmetic mean values of
are the arithmetic mean values of ![]() and
and ![]() . With the method of least squares we can make a linear regression that approximates the relationship with a linear function
. With the method of least squares we can make a linear regression that approximates the relationship with a linear function ![]() .
.![]()
![]() of the linear regression function
of the linear regression function ![]() is given by:
is given by: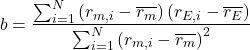
![]() and
and ![]() is given by:
is given by: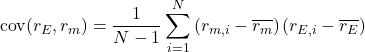
![]() is given by:
is given by: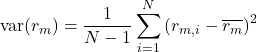
![]() leads to:
leads to:![]()
![]() ) in the Capital Asset Pricing Model (CAPM). That means that
) in the Capital Asset Pricing Model (CAPM). That means that ![]() is the slope of the linear approximated relationship of equity return rate
is the slope of the linear approximated relationship of equity return rate ![]() and market return rate
and market return rate ![]() using the method of least squares. In linear approximation we can state:
using the method of least squares. In linear approximation we can state:![]()
![]() . This point of view is valid for all betas in general.
. This point of view is valid for all betas in general.