Real Options - Investment and Project Valuation

Binomial Model Probabilities

Joachim Kuczynski, 24 October 2023

Introduction

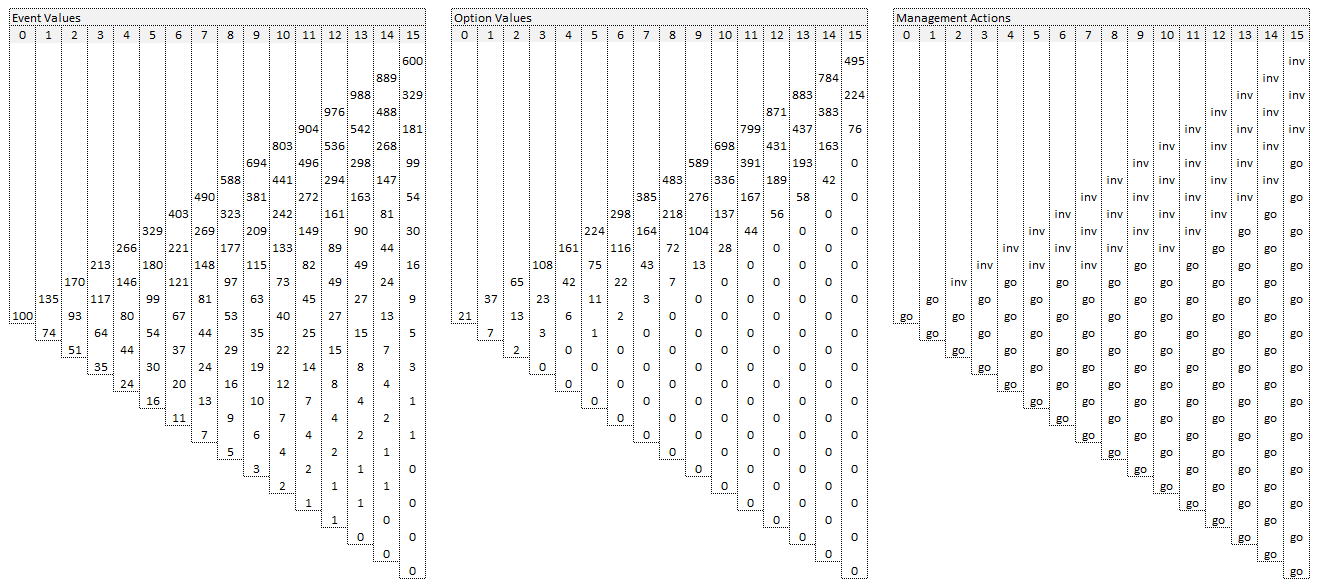
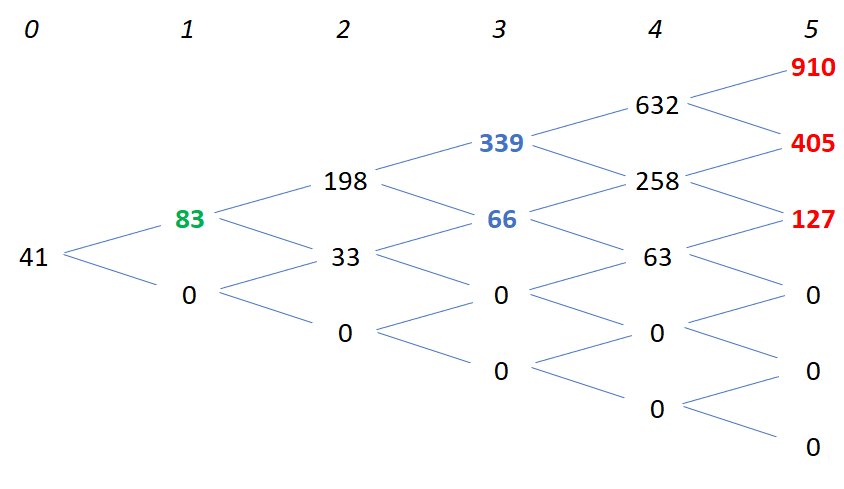
In this article I want to derive the explicit relationship between an option value and the probability of occurrence of its event states in the binomial model of Cox, Ross and Rubinstein. In many cases I read that the risk neutral probabilities and therefore the option value do not depend on the probabilities of the real state values. But the options values depend on them implicitly. That is what I will derive in this post.

Binomial Model by Cox, Ross and Rubinstein

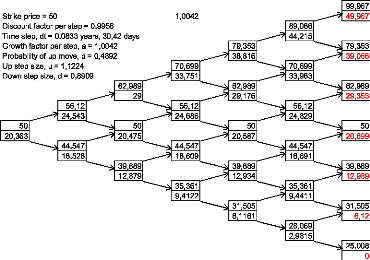
Options can be valued with the binomial model from Ross, Cox and Rubinstein. The value $C_0$ of an option at time $t_0$ is given by:

$C_0=\frac{\alpha C_{u,t_1}+(1-\alpha )C_{d,t_1}}{(1+r)^T }$

$C_{u,t_1}$ and $C_{d,t_1}$ are the option values of the up and down development at time $t=1$ . $r$ is the risk free rate and T is the time between $t_0$ and $t_1$ , $T=t_1-t_0$ . $\alpha$ is the risk neutral probability of the up movement in $t_1$ , $1-\alpha$ is the risk neutral probability of the down movement in $t_1$ . The binomial model provides the following relationship:

$\alpha=\frac{(1+r)^T-d}{u-d}$

Including $\alpha$ provides this expression for $C_0$

$C_0=\frac{\frac{(1+r)^T-d}{u-d} C_{u,t_1}+(1-\frac{(1+r)^T-d}{u-d} )C_{d,t_1}}{(1+r)^T }$

Hence we obtain:

$C_0=\frac{( (1+r)^T-d ) C_{u,t_1}+(u-(1+r)^T )C_{d,t_1}}{(1+r)^T (u-d)}$

$u$ and $d$ are defined as ratio of up and down movement in relation to the expected value in $t_0$ , $EV(S_{t_0})$ :

$u= \frac{EV(S_{t_0})}{S_{u,t_1}}$

$d= \frac{EV(S_{t_0})}{S_{d,t_1}}$

Up to now the probabilities of up state $S_{u,{t_1}}$ and down state $S_{d,{t_1}}$ have not occured. Many times that leads to the argument that these probabilities do not influence the option value. But that is not true. The expected value of the state $S_{t1}$ and therefore $S_{t0}$ depends on the probabilities. The expected value of the event state in $t_0$ is the discounted value of event state in $t_1$ . With $D$ as yearly constant discount rate we get:

$EV(S_{t_0})=\frac{EV(S_{t_1})}{(1+D)^T}=\frac{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}{(1+D)^T}$

For $u$ and $d$ we get the following:

$u=\frac{EV(S_{t_0})}{S_{u,t_1}}=\frac{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}{S_{u,t_1}(1+D)^{T}}$

$d=\frac{EV(S_{t_0})}{S_{u,t_1}}=\frac{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}{S_{d,t_1}(1+D)^{T}}$

As final result we obtain:

$C_0=\frac{( (1+r)^T-\frac{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}{S_{d,t_1}(1+D)^{T}}) C_{u,t_1}}{(1+r)^T ( \frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{d,t_1}(1+D)^{T}}})}+$

$+\frac{(\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-(1+r)^T )C_{d,t_1}}{(1+r)^T ( \frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{d,t_1}(1+D)^{T}}})}$

This is the basic relationship between the value of an option at a time $t_0$ and explicit problem specific variables.

Conclusion

We realize that the option value $C_0$ expicitely depends on the probability $p$ of the up state $S_{u,t_1}$ , and $1-p$ of the down state $S_{d,t_1}$ respectively. That is what we wanted to prove. The argument that this dependency does not exist, does not take into account that the value of state $S_0$ depends on the state probabilities in $t_1$ . Hence there is no disappearance mystery of real life or real states probabilities in options valuation. q.e.d.

Binomial Model vs. Black Scholes

Joachim Kuczynski, 06 December 2022

There are two basic ways to evaluate real options. The first way is the evaluation with exact analytical approaches like the famous Black Scholes Merton model. They have their origin in financial option pricing and deliver exact results. But they have certain underlying conditions that do not match reality of real options many times. The second basic approach to evaluate real options are discrete approximative models like the Binomial Model from Cox, Ross and Rubinstein. They are approximations of the exact analytical solutions when they have the same underlying conditions. In my real option analysis I prefer the approximative approach because of many reasons:

Volatility: The volatility, or risk respectively, defines the variance of the binomial tree branches (ups and downs). Volatility can change over time because of many reasons. But in the Black Scholes Merton model volatility is fixed for the considered time interval. Taking the binomial approach it is up to you to change volatility whenever you want. For sure, the binomial tree can become more complicated, e.g. if you have to change from a recombining to a non-recombining binomial tree. But with computer support also a more complicated event tree is no problem.
Exercise price: The exercise price at a node is the time value of the corresponding future cash flows which do not depend on the market development and are not diversiviable (mainly investments, fixed expenses and fixed earnings). Each of these components can change in time. That means that the exercise price of the real option can be differerent in each period. In the Black Scholes Merton model the exercise price is the same over time. In case of changing exercise prices you have to use approximative (binomial) approaches.
Discount rates: The discount rate includes many parameters like risk free rate, non-diversifiable market risks of the cash flow, the investor’s capital structure, the investor’s opportunity portfolio and tax shields. All these parameters can vary over time, and hence change the discount rate. If the discount rate changes, you might get a non-recombining binomial tree. Take care that the discount rate in each period has to match the expected values of the binomial tree branches in each period.
Decision tree: The decision tree does not have to be a complete binomial tree as required at the approximation of the Black Scholes Merton approach. Some branches might not exist or there can be more than one possibility in a node of the binomial tree (tri- or multinomial trees). Sometimes these exceptions represent reality more accurately and can be calculated in a discrete model. But these cases are not an approximation of Black Scholes Merton model any more. The Black Scholes Merton model cannot handle such tasks.
Time steps: Times between nodes of an event tree can be different at each link. You can adapt the times to your specific problem if required. The nodes of the event tree can for example be determined by the decision time of the investment project. At the Black Scholes approach the temporal development is fixed by the input parameters. There is no possibility to adapt it anyway. In the binomial approach you can adapt time steps as required by the corresponding problem.

In general, the (binomial) approximative approaches are much more flexible and can be adjusted to the specific problem. With specific input parameters the binomial model is an exact approximation of the Black Scholes Merton model. But many times the input parameters describing reality are different. Black Scholes Merton comes from financial option markets, where situations are less complex as at real options many times. The binomial approach is much more suitable for real option analysis. Because of the inaccuracy of many input variables at real options, the approximative character of the binomial model does not distort the result mostly.

Investment Term

In this post I would like to make some comments concerning the term INVESTMENT. It is a central notion in investment and project valuation. Many key figures are based on this term. Hence it is important that we really know what it is.

An asset valuation is always done from the fund / capital providers’ or investors’ sight. From that point of view an investment is the amount of cash that the investor has to provide to run the investment project. The cash flow between investor and investment project is the basis of the valuation. Thereby it is not important when the investment cash flow takes place. An investment cash flow does not has to be an initial cash flow in the beginning of the project. An investor can always shift the cash flows by using the capital markets. He can borrow money from a bank and pays it back later with additional interests.

From the investor’s point of view it is not important how the cash is handled in the income statement and balance sheet. The investor is only interested in cash flows concerning him / her. The notion investment does not depend on any classification in income statement and balance sheet. Further it is irrevelant whether the investment cash flow is depreciated / amortized or not.

The investment of a project are all fixed cash flows. That are all cash flows that have no dependency on the market devopment. These are for example cash flows for machines, land, buildings, product development, fixed costs for production, patents, fixed customer payments for various items and further more. It is not important whether these cash flows are incoming or outgoing. In a discounted cash flow analysis the investment cash flows must be discounted with the riskless rate that includes no risk premium. It is incorrect to discount investment cash flows with any discount rate including market risk premiums, for example the WACC. For that reason all figures valuing a project with a single rate (IRR, MIRR, …) are doubtful. They cannot value projects with cash flows having different risk and with it discount rates.

All cash flows that depend on the market development are not investment cash flows. That mainly includes turnover and variable costs. They must be discounted with the appropriate risk adjusted discount rate, because the investor requires a risk premium for taking that non diversifiable risks. Each risky cash flow has its specific own risk and requires an appropriate risk adjusted discount rate.

Matching Volatility in Binomial Model

Let us consider one step of a CRR binomial model with time interval $\Delta t$ , initial state $S_0$ in $t=0$ , an up-state of $S^+=S_0u$ in $t = \Delta t$ and a down state of $S^-=S_0d$ in $t= \Delta t$ . The probability of an up movement is assumed to be $p$ , the probability of a down movement $1-p$ respectively, with $0<p<1$ . The expected value after the first time step $\Delta t$ is $S_0 exp( \mu \Delta t)$ and has to be the same as the expected value of the two binomial states in $\Delta t$ :

$p S_0 u + (1-p) S_0 d=e^{\mu \Delta t}$

Let $E(X)$ be the expected value of a random variable $X$ . Then the variance $var(X)$ of $X$ equals to $var(X)=E(X^2)-[E(X)]^2.$ With that the variance of the two states of the binomial tree in $\Delta t$ is:

$pS_0^2 u^2+(1-p) S_0^2 d^2-(puS_0+(1-p)dS_0 )^2$

A stock price, or a project value (for real options analysis) respectively, follows a Geometric Brownian motion (stochastic Wiener process). Let $\sigma$ be the expected annual volatility of the process. $\sigma$ is defined as standard deviation of the normal distribution $\Phi$ of the annual relative returns:

$\frac{ \Delta S}{S} \thickapprox \Phi ( \mu \Delta t, \sigma \sqrt{\Delta t})$

The variance of such a Geometric Brownian motion is:

$var(S)=S^2 \sigma ^2 \Delta t$

Our binomial model should match the parameters of the continuous model. Therefore the variance of the binomial model and the variance of the Geometric Brownian motion have to be the same. Hence we get the following equation:

$p u^2 + (1-p) d^2 - ( p u+ (1-p) d)^2 = \sigma ^2 \Delta t$

In my point of view this is a very important expression, because it determines the correlation of u and d to match volatility. When terms in $\Delta t^2$ and higher powers of $\Delta t$ are ignored, one solution of this equation is:

$u=e^ {( \sigma \sqrt {\Delta t})}$

$d=e^ {( - \sigma \sqrt {\Delta t})}$

These are the values of $u$ and $d$ proposed by Cox, Ross and Rubinstein in their Binomial Model for matching $u$ and $d$ . But in principle there are infinite possible solutions of this equations. If you define an up or down movement, you can calculate the other value approximative numerically, e.g. with the goal seek function in Excel, even though there might be no closed solution.

Additionally it can be proofed that the variance does not depend on the expected return $\mu$ , when $\Delta t$ tends to zero. That means that the volatility is independent from the expected return. This is known as Girsanov’s theorem. When we move from a world with one set of risk preferences to a world with another set of risk preferences, the expected growth rates in variables change, but their volatilities remain the same.

Switch Options to Shut Down Example

Problem Framing

In this post I want to give a simple example of a switch option to shut down operations. Project management can decide each year whether to continue production or shut down operations in this year. If operations is shut down, management can generate cost savings by reducing fixed costs. If considered production continues, the project can generate additional revenues and contribution cash flows.
The project lifetime is 10 years, the WACC of the market contribution cash flows is 10.0% and constant over time. The contribution cash flows are shown in the graph below. The default (or risk) free rate is 5.0%. The switches between the mode of operation to the mode of shut down require costs in both directions. Switch costs, contribution cash flows and savings are shown in the table. Savings and switch costs increase with an inflation rate of 1.5% per year.

Swith Option to Shut Down Valuation

We want to give answers to the following questions: What is the value of this option to switch between the two modes? When do we have to switch between operation and shut down to get the maximum value added to the project?

DCF analysis provides a present value of the market contribution cash flows of 461 million EUR. A Monte-Carlo-Simulation provides a project volatility of 0.30. We want to analyze this switch option with the binomial approach of Cox-Ross-Rubinstein. As time periods we take one time step per year, so that you can read the figures in the lattice properly. For higher accuracy we could take smaller time periods anytime.

Below you can have look at the two binomial lattices. The first value at each node is the value of the underlying (market contribution cash flows). The second value is the value of the underlying including the switch option value. In the third line you can see whether you have to take the option and switch to the other mode or not. “Sw” means to switch to the other mode, “go” means to stay in the mode.

Binomial tree of the project’s active operation mode

Binomial tree of the project’s shut down mode

Beginning the project with the mode of operation (production), the value of the project including the option is 513 MEUR. That is 52 MEUR higher than the value of the project without any option (461 MEUR). Hence the option adds a value of 52 MEUR to the project, the ROV (real option value) is 52 MEUR. That is also the maximum that project management should invest in having the option. If you start the project with the shut down mode, the value added is only 33 million EUR.

The value added of 52 million EUR means that the NPV of the classical DCF analysis may convert from negative to positive because of this additional value. That could lead to a reconsidering of the project decision. The ENPV (expanded NPV) is the NPV of the project plus the value of the switch option. The savings of the shut down mode must be separate outgoing cash flows of the DCF analysis. They have to be discounted with the default free discount rate of 5.0%, because the savings are part of the project’s fixed costs. That is consistent to the component cash flow procedure (CCFP) approach. Investment and fixed costs cash flows have to be discounted with the default (or risk) free discount rate and not with the WACC of the market contribution cash flows.

In the binomial lattices you can also see what you have to do in which situation in the 10 years. Depending on the economic development, you should stay in the mode or switch to the other mode. This is a practical guideline for project management.

Additional Remarks

I constructed the event tree of the project’s contribution cash flows out of a Monte-Carlo-Simulation. Of course you can also create the nodes of the event trees by calculating the time values of the outstanding contribution cash flows explicitly. Discussion with management and marketing can provide the required cash flows and probabilities of the event tree. Analytical valuation methods like Black-Scholes-Merton cannot provide any solution for option types like this.

Option to Choose Example

Problem Framing

In this post I want to give a simple example of a choose option valuation. The considered project lasts 10 years, the WACC of the contribution (market) cash flows is 10.0% and constant over time. The contribution cash flows are shown in the graph below. Let the risk free rate be 5.0%. The project provides 3 options: 1) Option to expand with an investment of 100 kEUR (increasing with an inflation rate of 2% per year). The contribution cash flows would be increased by 20%, if managements invests in the expansion. 2) Option to abandon the project with a salvage value of 100 kEUR (increasing with an inflation rate of 2% per year) and 3) Option to contract with a savings of 200 kEUR (increasing with an inflation rate of 2% per year) and a contraction factor of 0.9. DCF analysis provides a present value of the market contribution cash flows of 1 million EUR. A Monte-Carlo-Simulation shows a project volatility of 0.30. We analyze this choose option with the binomial approach of Cox-Ross-Rubinstein. As time periods we take two time steps per year, so that you can read the figures in the lattice properly. For higher accuracy we could take smaller time periods anytime.

Choose Option Valuation

We want to give answers to the following questions: What is the value of this option to choose? When do we have to take which option to get the maximum value added for the project?

We take the binomial approach from Cox-Ross-Rubinstein to solve that issue. Following you can have look at the binomial lattice. The first value of each node is the value of the underlying (market contribution cash flows). The sevond value is the value of the options at this node. In the third line you can see whether you have to take an option and which option you have to take. “exp” means to invest in the expansion of the project, “go” means to take no option at this node and “con” means to invest in the contraction of the project.

The total value of the three options is 137 kEUR. That is the maximum investment that should be done for the three options in sum. The option to abandon is not taken in any node. That means that you should not invest in this abandonment option. In the first year you should not take any option, let the project evolve. In the second year there might be the first opportunities to take the expansion option. In the following years the expansion option is a good opportunity in case of positive cash flow development. Your project controlling should have a look at the cash flow development and go the right path through the lattice over time. In the first six years the contraction option provides no addition value to the project. But in the last three years of the project the contraction option becomes more important.

Note that this choose option adds a value of 137 kEUR to the project. That means that the NPV of the classical DCF analysis can convert from negative to positive because of the additional value. That could lead to a reconsidering of the project decision. The ENPV (expandedNPV) is the NPV of the project plus the value of the choose option.

Additional Remarks

I constructed the event tree from the project’s contribution cash flow volatility out of a Monte-Carlo-Simulations. Of course you can also create the nodes of the event trees by calculating the time values of the outstanding contribution cash flows explicitly. Discussion with management and marketing can provide the required cash flows and probabilities of the event tree.

This option to choose combines the three options of expansion, contraction and abandonment. This example also shows that the value of various options is not the sum of its individual options. Although the option to abandon has an option value by itself, it contributes no additional value to the option to choose, because it is not required in any node. Analytical valuation methods like Black-Scholes-Merton cannot provide exact solutions for such interdependent options.

Option to Switch Example

Problem Framing

In this post I want to give a simple example of a swich option valuation. The considered project lasts 10 years, the WACC of the contribution (market) cash flows is 10.0% and constant over time. The contribution cash flows are shown in the graph below. Let the risk free rate be 5.0%. The project provides 2 operation modes (possibilities), one with technology A and the other with technology B. A Monte-Carlo-Simulation of technology A shows a project’s contribution cash flow volatility of 0.30. The corresponding Monte-Carlo-Simuation of technology B provides a project’s contribution cash flow volatility of 0.15. We analyze this switch option with a binomial approach. As time periods we choose one time step per year, so that you can read the figures in the lattices. For higher accuracy we could take smaller time periods anytime. The present value of the project market contribution cash flows is 1 million USD. Switch costs from technology A to B start with 145 kUSD, from technology B to A start with 80 KUSD. These costs increase with an inflation rate of 2.0%.

Switch Option Valuation

We want to give answers to the following questions: What is the value of this option to switch between technology A and technology B? How much can we invest in this flexibility keeping a positive added value to the project? And when do I have to switch between the 2 technologies to get the maximum value added?

We take the binomial approach from Cox-Ross-Rubinstein to solve that issue. Following you can have look at the binomial lattices for both technologies. The first value of each node is the value of the underlying (market contribution cash flows), the sevond value is the value of the switch option at the corresponding node. In the third line you can see whether you have to switch to the other technology or not (“sw” means to switch, “go” means to stay in the technology).

Binomial tree of switch option for technology A

*Binomial tree of switch option for technology* B

The value of the switch option starting with technology A is 21 kUSD. Starting with technology B the switch option value is 157 kUSD. If the investment for the switch option flexibility is below these option values, you should do the investment. If you can choose the starting technology, you should start with B. This results in a higher value added, the corresponding investments not taken into account. In the first year you have to make no switch in any case. In the second year it depends on the cash flow development, if you start with technology A. Switch in the bad case to technology B and stay in technology A in case of positive development. Starting with technology B you should stay there and make no switch, independent of the cash flow development. In the third year you should switch to technology A in the best cash flow development. Analyzing the event/option tree through time in this way provides a guideline for what to do in which year, depending on the cash flow development.

Note that this switch option adds a value of 157 kEUR to the project. That means that the NPV of the classical DCF analysis can convert from negative to positive because of this additional value. That could lead to a reconsidering of the project decision. The ENPV (expanded NPV) is the NPV of the project plus the value of the switch option.

Additional Remarks

I constructed the event tree from the project’s contribution cash flow volatilities out of Monte-Carlo-Simulations. Of course you can also create the nodes of the event trees by calculating the time values of the outstanding contribution cash flows explicitly. Discussion with management and marketing can provide the required cash flows and probabilities of the event tree.

This switch option valuation approach can be applied to many problems with different operation possibilities. Switch options are compound options with path-dependency. They are a good examples that real options can be more complicated than financial options. Analytical valuation methods like Black-Scholes-Merton cannot give you a solutions for problems like that.

Replication Portfolio in Binomial Model

In this post I a want to give a short derivation of the replication portfolio and the risk neutral probabilities in the binomial model from Cox-Ross-Rubinstein. Let $V$ be the value of the underlying asset in $t_0$ . In a project or investment this might be the present value of the project’s contribution (market related) cash flows. The positive development of $V$ at time $t_1$ , $V^+$ , occurs with probability $p$ , the negative development with value $V^-$ in $t_1$ with probability $1-p$ . The twin security of the underlying in the open market takes a similar notation $S$ , $S^+$ , $S^-$ , $p$ . We consider an option with option value $E$ in $t_0$ that leads to an option value of $E^+$ in the upper state $V^+$ and to an option value of $E^-$ in the lower state $V^-$ . As result we are searching the option value $E$ at time $t=0$ .

Next we replicate the option value in $t_1$ by a portfolio of $n$ shares of twin security $S$ partly financed by borrowings of amount $B$ at the risk-free rate $r$ . The values of the upper and lower state in $t_1$ are $E^+=nS^+-\left(1+r\right)B$ and $E^-=nS^--\left(1+r\right)B$ .

In efficient markets there exist no profitable arbitarge opportunities. Therefore the outcome of the option value $E$ in $t=1$ must be the same in the upper and in the lower state. Setting $E^+-nS^+=E^--nS^-$ we get:

$n=\frac{E^+-E^-}{S^+-S^-}$

Replacing $n$ in the previous equations we obtain the value borrowed at the risk-free rate r:

$B=\frac{1}{1+r}\frac{{E^+S^--E}^-S^+}{S^+-S^-}$

The law of one price tells us that the value of assets that lead to the same cash flows must be the same. That means that the value of the option at time $t_0$ must be the same as the value of the portfolio at time $t_0$ . Therefore we can set $E=nS-B$ . With that we calculate the value of the option in $t_0$ :

$E=\frac{\left(\frac{S\left(1+r\right)-S^-}{S^+-S^-}\right)E^++\left(1-\frac{S\left(1+r\right)-S^-}{S^+-S^-}\right)E^-}{1+r}$

We create a new variable $p^\prime$ to simplify the previous expression.

$p^\prime=\frac{S\left(1+r\right)-S^-}{S^+-S^-}$

Hence we obtain:

$E=\frac{p\prime E^++\left(1-p\prime\right)E^-}{1+r}$

$p^\prime$ can be interpreted as probability for $E^+$ , $1-p^\prime$ for $E^-$ . $p^\prime$ and $1-p^\prime$ are known as risk-neutral probabilities. Note that the value of the option does not explicitly involve the actual probabilities $p$ and $1-p$ of the underlying. Instead, it is expressed in terms of risk-neutral probabilities. They allow to discount the expected future values at the risk-free rate.

Discounting at the risk-free rate is the main difference between decision tree analysis (DTA) and contingent claim analysis (CCA) or real options analysis (ROA). DTA does not take into account that the risk of the cash flow streams changes when you consider options and opportunities. ROA implements this issue correctly.

Option to Wait

This is a simple example of an option to wait. We consider a 15 year project which requires an investment of 105 M€, that can be done anytime. Arbitrage Pricing Theory provides a yearly risk-adjusted capital discount rate (WACC) of 15%. Investment and internal risk cash flows are discounted by the risk-free rate. We assume for all years equal free net cash flow present values of 100/15 M€. Classical incremental cash flow analysis provides a present value of the market-related net cash flows of 100 M€. That means that the classic NPV of the project is -5 M€. Because of the negative NPV management should reject the project.

But management has an option to wait. It can wait with the decision and invest only if the market development is profitable. For sure the company loses revenues because of the delayed investment, but on the other hand management gets more information about market development. The question is: What is the value of this option to wait and how long should management wait with that investment decision? Can the project become profitable?

Monte-Carlo-Simulation of the project provides a project volatility of 30%. The risk-free rate is 5%. Next we are performing a real option analysis (ROA) of the waiting option with the binomial approach regarding 15 time steps, one for each year.

Real option analysis provides a project value of 21 M€. That means that the value added by the waiting option is 26 M€. Because the project value with waiting option is positive we should not reject the project any more. Management should go on with the project. Including the option in the project valuation leads to the opposite management decision. And besides the waiting option there might be additional options like the option to abandon or the option to expand/contract. They would bring additional value to the project.

Real option analysis also provides the information that there should be no investment done before the second year. Dependent from the market development management can decide when to invest according to the time value of the expected free cash flows.

In this example we assumed yearly cash flows that results in a decrease of the expected future cash flows. This corresponds to paying dividends at financial securities. Considering options in the lifetime of a project requires binomial valuation with leakage. If you assume relative leakage you get a recombining tree, with absolute leakage values you get a non-recombining binomial tree.

Sequential Compound Options

This is a simple example of a sequential compound option, which is typical in projects where the investment can be done in sequential steps. The option is valued by the binomial approach.

The project is divided into three sequential phases: (1) Land acquisition and permitting, (2) design and engineering and (3) construction. Each phase must be completed before the next phase can start. The company wants to bring the product to market in no more than seven years.
The construction will take two years to complete, and hence the company has a maximum of five years to decide whether to invest in the construction. The design and engineering phase will take two years to complete. Design and engineering has to be finished sucessfully before starting construction. Hence the company has a maximum of three years to decide whether to invest in the design and engineering phase. The land acquisition and permitting process will take two years to complete, and since it must be completed before the design phase can begin, the company has a maximum of one year from today to decide on the first phase.
Investments: Permitting is expected to cost 30 million Euro, design 90 million Euro, and construction another 210 million Euro.
Discounted cash flow analysis using an appropriate risk-adjusted discount rate values the plant, if it existed today, at 250 million Euro. The annual volatility of the logarithmic returns for the future cash flows for the plant is evaluated by a Monte-Carlo-Simulation to be 30%. The continuous annual risk-free interest rate over the next five years is 6%.
Static NPV approach: The private risk discount rate for investment is 9%. With that we get a NPV without any flexibility and option analysis of minus 2 million Euro. Because of its negative NPV we would reject the project neglecting any option flexibility.
ROA: Considering the real options mentioned above we calculate a positive project value of 41 million Euro. That means that the compound options give an additional real option value (ROV) of 43 million Euro. Thus we should implement the project.

The real option analysis additionally provides the information when and under which market development to invest in each phase. The investment for the first phase should be done in year 1, for the second phase in year 3 and for the third phase in year 5. The option valuation tree tells management what to do in which market development.
The valuation can be done in smaller time steps to increase accuracy. But the purpose of this example is to illustrate the principle of a sequential compound option valuation.
Details are specified in Kodukula (2006), p. 146 – 156.

CRR Binomial Method

Das Binomialmodell von Cox-Ross-Rubinstein aus dem Jahr 1979 ist der Grundstein für die klassische Optionsbewertung von Finanztiteln. Aber auch für die Bewertung von Realoptionen ist es das zentrale Modell, mit welchem flexibel unterschiedliche Optionsarten simultan analysiert werden können.

Cox-Ross-Rubinstein-1979 Herunterladen

Quelle: https://imgv2-1-f.scribdassets.com/img/document/172618676/original/bc67d26ed3/1584997045?v=1