Problem Framing
In this post I want to give a simple example of a choose option valuation. The considered project lasts 10 years, the WACC of the contribution (market) cash flows is 10.0% and constant over time. The contribution cash flows are shown in the graph below. Let the risk free rate be 5.0%. The project provides 3 options: 1) Option to expand with an investment of 100 kEUR (increasing with an inflation rate of 2% per year). The contribution cash flows would be increased by 20%, if managements invests in the expansion. 2) Option to abandon the project with a salvage value of 100 kEUR (increasing with an inflation rate of 2% per year) and 3) Option to contract with a savings of 200 kEUR (increasing with an inflation rate of 2% per year) and a contraction factor of 0.9. DCF analysis provides a present value of the market contribution cash flows of 1 million EUR. A Monte-Carlo-Simulation shows a project volatility of 0.30. We analyze this choose option with the binomial approach of Cox-Ross-Rubinstein. As time periods we take two time steps per year, so that you can read the figures in the lattice properly. For higher accuracy we could take smaller time periods anytime.
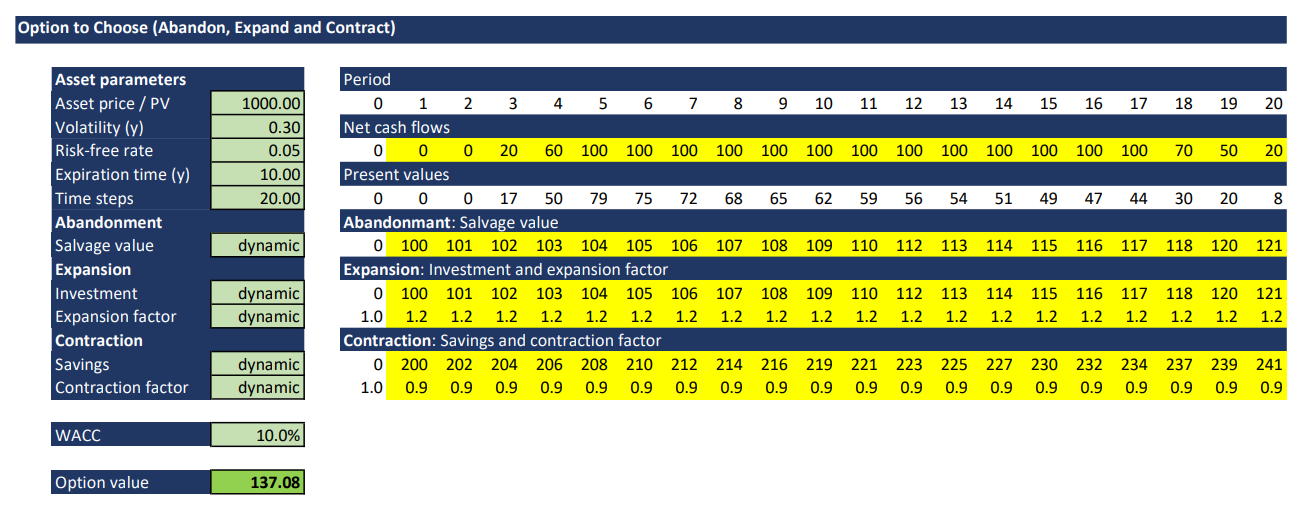
Choose Option Valuation
We want to give answers to the following questions: What is the value of this option to choose? When do we have to take which option to get the maximum value added for the project?
We take the binomial approach from Cox-Ross-Rubinstein to solve that issue. Following you can have look at the binomial lattice. The first value of each node is the value of the underlying (market contribution cash flows). The sevond value is the value of the options at this node. In the third line you can see whether you have to take an option and which option you have to take. “exp” means to invest in the expansion of the project, “go” means to take no option at this node and “con” means to invest in the contraction of the project.
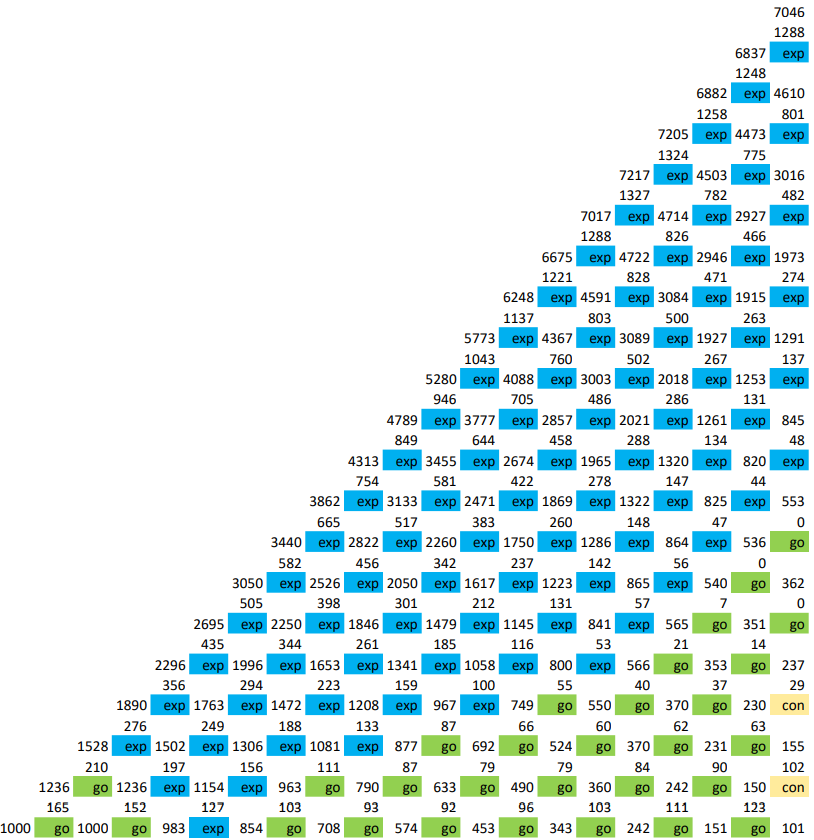

The total value of the three options is 137 kEUR. That is the maximum investment that should be done for the three options in sum. The option to abandon is not taken in any node. That means that you should not invest in this abandonment option. In the first year you should not take any option, let the project evolve. In the second year there might be the first opportunities to take the expansion option. In the following years the expansion option is a good opportunity in case of positive cash flow development. Your project controlling should have a look at the cash flow development and go the right path through the lattice over time. In the first six years the contraction option provides no addition value to the project. But in the last three years of the project the contraction option becomes more important.
Note that this choose option adds a value of 137 kEUR to the project. That means that the NPV of the classical DCF analysis can convert from negative to positive because of the additional value. That could lead to a reconsidering of the project decision. The ENPV (expandedNPV) is the NPV of the project plus the value of the choose option.
Additional Remarks
I constructed the event tree from the project’s contribution cash flow volatility out of a Monte-Carlo-Simulations. Of course you can also create the nodes of the event trees by calculating the time values of the outstanding contribution cash flows explicitly. Discussion with management and marketing can provide the required cash flows and probabilities of the event tree.
This option to choose combines the three options of expansion, contraction and abandonment. This example also shows that the value of various options is not the sum of its individual options. Although the option to abandon has an option value by itself, it contributes no additional value to the option to choose, because it is not required in any node. Analytical valuation methods like Black-Scholes-Merton cannot provide exact solutions for such interdependent options.
