Project WACC and Company WACC - Strategic Investments

Joachim Kuczynski, 14 November 2025

This article shows how to derive the WACC (weighted average cost of capital) of a project from the WACC of a company (or asset portfolio in general). Further on company and portfolio have the same meaning. Let us assume a company or portfolio with $n$ projects. The relative share of project $i$ in the portfolio is $\alpha_i$ . The WACC of project $i$ is $\omega_i$ . The cost of capital of the portfolio, $\omega_p$ , is given by:

(1) $\begin{equation*}\omega_p=\frac{\sum_{i=1}^{n}V_i\omega_i}{\sum_{j=1}^{n}V_j}=\sum_{i=1}^{n}\frac{V_i}{\sum_{j=1}^{n}V_j}\omega_i=\sum_{i=1}^{n}\alpha_i\omega_i\end{equation*}$

That means that the WACC of a portfolio is the weighted average of the components’ WACC.

Let us have a look at the variance of the portfolio WACC:

(2) $\begin{equation*}\mathrm{var}\left( \omega_p \right)=\mathrm{cov}\left( \omega_p,\omega_p \right)=\mathrm{cov}\left(\sum_{i=1}^{n} \alpha_i\omega_i, \omega_p \right)\end{equation*}$

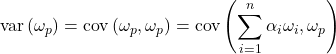
The covariance is bilinear, we get:

(3) $\begin{equation*}\mathrm{var}\left( \omega_p \right)=\sum_{i=1}^{n}\alpha_i\mathrm{cov}\left( \omega_i, \omega_p \right)\end{equation*}$

The correlation of an asset’s WACC $\omega_i$ with the portfolio’s WACC $\omega_p$ is defined by:

(4) $\begin{equation*}\mathrm{corr}\left( \omega_i,\omega_p \right):=\frac{\mathrm{cov}\left( \omega_i,\omega_p \right)}{\sigma\left( \omega_i \right)\sigma\left( \omega_p \right)}\end{equation*}$

$\sigma (\omega_i)$ and $\sigma (\omega_p)$ are the standard deviations of $\omega_i$ and $\omega_p$ . Substituting covariance by correlation we get:

(5) $\begin{equation*}\mathrm{var}\left( \omega_p \right) =\sum_{i=1}^{n}\alpha_i \sigma \left( \omega_i \right)\sigma\left( \omega_p \right)\mathrm{corr}\left( \omega_i, \omega_p \right)\end{equation*}$

Dividing by the standard deviation $\sigma\left( \omega_p \right)$ leads us to the standard deviation of the portfolio:

(6) $\begin{equation*}\sigma\left( \omega_p \right) =\sum_{i=1}^{n}\alpha_i \sigma \left( \omega_i \right)\mathrm{corr}\left( \omega_i, \omega_p \right)\end{equation*}$

That means that the incremental risk contribution of each project to the risk of the portfolio is $\sigma\left( \omega_i \right)\mathrm{corr}\left( \omega_i, \omega_p \right)$ and not just the weighted sum of its projects’ risks. Hence we can e.g. reduce the WACC of the portfolio by adding a project with negative correlation to the portfolio.\

Instead of including a new project to the portfolio the company can also increase the return of the portfolio by increasing the risk of the portfolio. This reward-to-volatility ratio of the tangential portfolio is given by the Sharpe Ratio:

(7) $\begin{equation*}\frac{E\left( \omega_p\right)-r_D}{\sigma \left( \omega_p \right)}\end{equation*}$

$E\left( \omega_p\right)$ is the expected value of $\omega_p$ and $r_D$ is the after-tax debt interest rate. The company wants to invest in the new project, if the additional WACC of this project is lower than an investment in the existing portfolio with the same risk changes. Hence we obtain the requirement to invest in the new project:

(8) $\begin{equation*}E\left( \omega_i \right)-r_D < \sigma\left( \omega_i \right)\mathrm{corr}\left( \omega_i,\omega_p \right)\frac{E\left( \omega_p\right)-r_D}{\sigma\left( \omega_p \right)}\end{equation*}$

With that we can define the sensitivity $\beta_i^p$ of the new project to the existing portfolio:

(9) $\begin{equation*}\beta_i^p:=\frac{\sigma\left( \omega_i \right)\mathrm{corr}\left( \omega_i,\omega_p \right)}{\sigma\left( \omega_p \right)}\end{equation*}$

Substituting with $\beta_i^p$ the requirement for the new investment becomes the well-known equation:

(10) $\begin{equation*}\text{E}\left( \omega_i \right) < r_D+\beta_i^p\left( E\left( \omega_p\right)-r_D \right)\end{equation*}$

With that we can define a maximum annual WACC of the additional project. This is the maximum WACC at which a company would decide to invest in the project.

(11) $\begin{equation*}\text{E}\left( \omega_i \right)^{max} = r_D+\beta_i^p\left( E\left( \omega_p\right)-r_D \right)\end{equation*}$

Let us assume that the new project and the company are correlated completely, which means $\mathrm{corr}\left( \omega_i,\omega_p \right)=1$ . In this case we get:

(12) $\begin{equation*}\text{E}\left( \omega_i \right)^{max} = r_D+\frac{\sigma\left( \omega_i \right)}{\sigma\left( \omega_p \right)}\left( E\left( \omega_p\right)-r_D \right)\end{equation*}$

The quotient $\sigma\left( \omega_i \right)/\sigma\left( \omega_p \right)$ is called relative risk factor of project $i$ . The risk premium of the company WACC is adapted by the quotient of the standard deviations of the project and the company. The higher the risk of the project the higher the required WACC of the project to become a new part of the company portfolio. If the risk of the project and the risk of the company are the same, the WACC of the project and the company are the same, too. The standard deviation can be generated by Monte Carlo Simulation or approximated by best/worst case scenarios. Another approach is to estimate the standard deviations by management. Instead of comparing the project to the whole company portfolio we can also compare it to a benchmark project. This benckmark project is considered to be representative for the company.