Joachim Kuczynski, 04 November 2025
This article is about an unusual sight on the CAPM beta. It provides a derivation from linear regression with the method of least squares. Often the definition of CAPM beta seems to be very abstract. But from the perspective of this article`s approach it might be clearer.
We assume a data set of market return rates ![]() and equity return rates
and equity return rates ![]() .
. ![]() indicates the
indicates the ![]() -th of
-th of ![]() data pairs.
data pairs. ![]() and
and ![]() are the arithmetic mean values of
are the arithmetic mean values of ![]() and
and ![]() . With the method of least squares we can make a linear regression that approximates the relationship with a linear function
. With the method of least squares we can make a linear regression that approximates the relationship with a linear function ![]() .
.
(1) ![]()
The slope ![]() of the linear regression function
of the linear regression function ![]() is given by:
is given by:
(2) 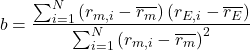
The covariance of ![]() and
and ![]() is given by:
is given by:
(3) 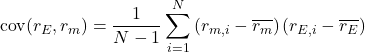
The variance of ![]() is given by:
is given by:
(4) 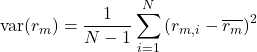
Substituting that in the expression for ![]() leads to:
leads to:
(5) ![]()
This is the same as beta (![]() ) in the Capital Asset Pricing Model (CAPM). That means that
) in the Capital Asset Pricing Model (CAPM). That means that ![]() is the slope of the linear approximated relationship of equity return rate
is the slope of the linear approximated relationship of equity return rate ![]() and market return rate
and market return rate ![]() using the method of least squares. In linear approximation we can state:
using the method of least squares. In linear approximation we can state:
(6) ![]()
In my point of view this is a very important point to know when doing investment analysis and using CAPM. It provides an additional interpretation of ![]() . This point of view is valid for all betas in general.
. This point of view is valid for all betas in general.
