Joachim Kuczynski, 27 November 2024
Die Bewertung von Investitionen und Projekten (bzw. allgemein Assets) basiert auf der Verschiebung und Anpassung von Cash Flows auf der Zeitachse. Geht diese Verschiebung rückwärts in der Zeit, so spricht man von Diskontierung. Eine Verschiebung vorwärts auf der Zeitachse nennt man Kapitalisierung. Viele Analysten verwenden für Diskontierung und Kapitalisierung in einem Projekt dieselbe Rate. Doch darf man die Cash Flows mit demselben Rate tatsächlich auf der Zeitachse vor und zurück schieben? Die Antwort darauf ist ein klares Nein.
Die Diskontierungsrate eines Cash Flows basiert auf seinem ihm innewohnenden Risiko (Volatilität). Im allgemeinen ist sie unabhängig von den Risikopräferenzen der Kapitalgeber, sofern dessen Anlagenportfolio ausreichend diversifierziert ist. Die Kapitalisierungsrate eines Cash Flows basiert hingegen auf den Risikopräferenzen und der Portfoliodiversifizierung des Unternehmens bzw. dessen Kapitalgeber. Die Kapitalisierungrate ist unabhängig davon, welches Risiko dem initialen Cash Flow innewohnte. Wenn er einmal zur Kapitalisierung zur Verfügung steht, spielt es keine Rolle, unter welchen Umständen er zustandekam. Diskontierungsrate und Kapitalisierungsrate sind prinzipiell ganz unterscheidlicher Natur. Sie in Kalkulationen gleichzusetzen ist grundlegender, logischer Fehler.
Es gibt Kennzahlen der Investitionsbewertung, die eine Rekapitalisierung rückfliessender Cash Flows beinhalten. Ein bekanntes Beispiel ist der Modifizierte Interne Zinssatz bzw. der Baldwin-Zins. Dort wird üblicherweise angenommen, dass Diskontierung als auch Wiederveranlagung mit dem WACC erfolgen. Der WACC basiert auf der Renditeerwartung der Kapitalgeber. Diese müssen sich aber keineswegs mit den Renditemöglichkeiten des investierenden Unternehmens decken. Oft werden zur Diskontierung zudem zusätzliche Raten („risk premium“) addiert. Damit möchte man beispielsweise Währungs- oder Standortrisiken berücksichtigen. Nimmt man nun dieselbe Rate auch für die Kapitalisierung, unterstellt man eine erhöhte Wiederveranlagungsrate für das Unternehmen. Dies ist natürlich falsch und erhöht den Fehlerhaftigkeit der Kalkulation weiter.
Zusammenfassend kann man festhalten, dass eine Gleichstellung von Diskontierungsrate und Kapitalisierungsrate grundlegend falsch ist. Viele Formeln lass sich mit einer Gleichsetzung zwar bequem vereinfachen. Die Ergebnisse der Kalkulation sind aber damit nicht mehr valide. Richtige und aussagefähige Ergebnisse der Investitionsrechnung sind jedoch die Grundlage für richtigen Investitionsentscheidungen.
![Rendered by QuickLaTeX.com \[MIRR=\sqrt[n]{\frac{\text{FV(contribution cash flows,WACC)}}{\text{PV(invest cash flows, financing rate)}}}-1\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-bc3151b9811774776aaad69dd41965ad_l3.png)
![Rendered by QuickLaTeX.com \[r=\frac{1}{t}ln\frac{C(t)}{C(0)}=\frac{1}{t}ln\left( \sum_{i}^{} \left \frac{C_i(0)}{C(0)} exp \left( r_i t \right) \right \right)\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-fb659cb84b82fa3fac2f0009b503dd4b_l3.png)
![Rendered by QuickLaTeX.com \[r\simeq \frac{1}{t}\left( \sum_{i}^{} \left( \frac{C_i(0)}{C(0)} \left( 1+ r_i t \right) \right) -1 \right)\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-87db3d07482630425a989b6495027b30_l3.png)
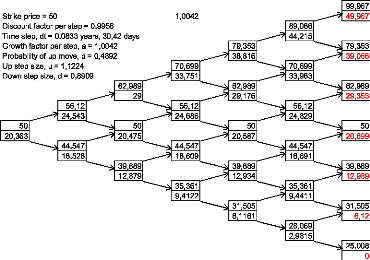
![Rendered by QuickLaTeX.com \[C_0=\frac{\frac{(1+r)^T-d}{u-d} C_{u,t_1}+(1-\frac{(1+r)^T-d}{u-d} )C_{d,t_1}}{(1+r)^T }\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-4585ecf3307b3ea36a992a134bd156a8_l3.png)
![Rendered by QuickLaTeX.com \[C_0=\frac{( (1+r)^T-\frac{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}{S_{d,t_1}(1+D)^{T}}) C_{u,t_1}}{(1+r)^T ( \frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{d,t_1}(1+D)^{T}}})}+\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-0769b16c961ea4a991747ee6dec7ad23_l3.png)
![Rendered by QuickLaTeX.com \[+\frac{(\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-(1+r)^T )C_{d,t_1}}{(1+r)^T ( \frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{u,t_1}(1+D)^{T}}}-\frac{{pS_{u,{t_1}}+(1-p)S_{d,{t_1}}}}{{S_{d,t_1}(1+D)^{T}}})}\]](https://www.financeinvest.at/wp-content/ql-cache/quicklatex.com-5b78a3049855170fe758d7f83b5e5355_l3.png)